vxgi
Real Time Global Illumination Using Voxel Cone Tracing

Global illumination (GI) adds realism to computer graphics by simulating how light interacts with surfaces. Traditional raytracing methods for GI are computationally expensive, leading to slower performance. To address this, Voxel Cone Tracing (VCT) offers a balance between performance and visual quality by approximating indirect lighting through cone tracing. Below, I detail the pipeline and techniques used in my project.
The VXGI Pipeline
Voxel Cone Tracing operates on a hybrid rendering pipeline:
- Voxelization is achieved using GPU hardware rasterization.
- Primary rays are rasterized for direct lighting.
- Secondary rays are cone-traced to compute indirect global illumination.
Voxelization Process
Voxelization is central to this technique, converting 3D geometry into a voxel representation for lighting computations. The process includes:
Rasterization:
- The GPU generates voxels, with thin-surface voxelization ensuring accuracy.
- Conservative rasterization ensures fragments are created for all pixels intersecting a primitive using NVIDIA’s
GL_NV_conservative_rasterextension.
Dominant Axis Projection:
- Triangles are projected along their dominant axis for efficient voxelization.
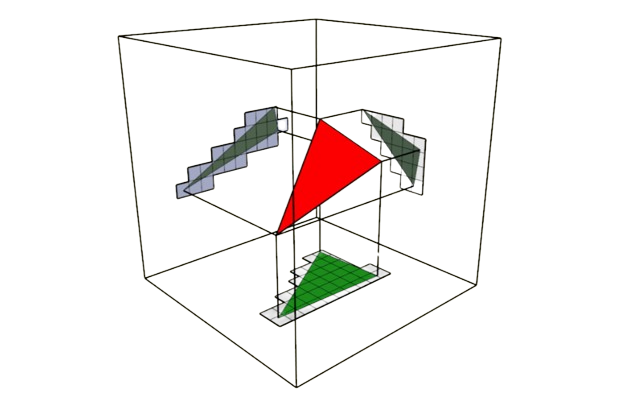
- Inside the Geometry Shader
// select the dominant axis
float axis = max(geometryNormal.x, max(geometryNormal.y, geometryNormal.z));
if (axis == geometryNormal.x) {
gl_Position = vec4(outputPosition.zy, 1.0, 1.0);
} else if (axis == geometryNormal.y) {
gl_Position = vec4(outputPosition.xz, 1.0, 1.0);
} else if (axis == geometryNormal.z) {
gl_Position = vec4(outputPosition.xy, 1.0, 1.0);
}
EmitVertex();
Direct Light Injection and Mipmapping:
- Direct lighting is computed and stored in a 3D image using OpenGL’s
imageStore(). - Automatic mipmap generation with
glGenerateMipmap()handles multi-resolution sampling.
Cone Tracing for Global Illumination
Cone tracing approximates the rendering equation for indirect lighting:
\[L_o(\mathbf{p}, \omega_o) = L_e(\mathbf{p}, \omega_o) + \int_{\Omega} f(\mathbf{p}, \omega_i, \omega_o) \cdot L_i(\mathbf{p}, \omega_i) \cdot (\mathbf{n} \cdot \omega_i) \, d\omega_i\]This integral is replaced by a summation of N cones.
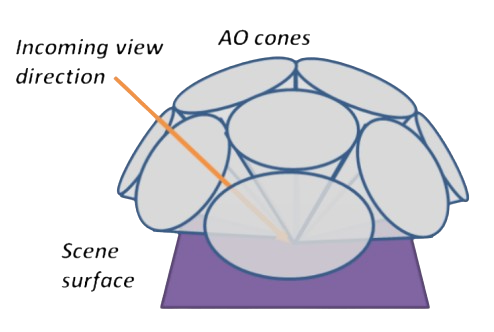
Each cone is raymarched through the voxelized 3D mipmap.

We define the diameter d as:
\[d = 2t \times \tan(\frac{\theta}{2})\]Sampling uses mipmap levels determined by:
\[V_{\text{level}} = \log_2(\frac{d}{V_{\text{size}}})\]Lighting values are accumulated volumetrically using alpha blending:
\[C = \alpha C + (1 - \alpha)\alpha_2C_2\] \[\alpha = \alpha + (1 - \alpha)\alpha_2\]Indirect Light Components
Results

